Метод ветвей и границ (МВГ) относится к группе комбинаторных методов, основную идею которых составляет замена полного перебора всех решений их частичным перебором, что осуществляется путем отбрасывания некоторых подмножеств вариантов, то есть допустимых решений, заведомо не дающих оптимума; перебор при этом ведется лишь среди остающихся вариантов, являющихся в определенном смысле «перспективными». Таким образом, основная идея всех методов ветвей и границ при всем их разнообразии базируется на использовании конечности множества вариантов и переходе от полного перебора к сокращенному (направленному) перебору. Важную роль при этом играют правила оценки и отбрасывания неперспективных множеств вариантов.

Метод ветвей и границ в случае точного вычисления оценок относится к точным методам решения задач выбора и потому в неблагоприятных ситуациях может приводить к экспоненциальной временной сложности. Однако метод часто используют как приближенный, поскольку можно применить приближенные алгоритмы вычисления оценок.

Перечислим основные этапы решения задачи методом МВГ.

1)   Трансформация задачи (ТЗ). Исходную задачу заменяют другой задачей так, что множество решений исходной задачи содержится в множестве решений трансформированной задачи. Найти оптимальное решение трансформированной задачи значительно проще, чем решение исходной задачи.

2)   Построение дерева решений. Множество решений ТЗ разбивают на подзадачи. Затем каждую подзадачу в свою очередь разбивают на подзадачи. В результате получается дерево решений. Процесс разбиения прекращается, если подзадача содержит не более одного решения исходной задачи, такая задача называется концевой. Если в результате работы МВГ будет построено полное дерево решений, то МВГ будет эквивалентен полному перебору, чем лучше работает МВГ, тем он дальше от полного перебора.

3)   Получение нижних оценок каждая подзадача трансформированной задачи содержит какое-то число решений исходной задачи (плата за упрощение). Отсюда оптимальное решение подзадачи меньше или равно лучшему из решений исходной задачи, содержащихся в этой подзадаче. Поэтому оптимальное решение трансформированной подзадачи называют оценкой снизу для решений исходной задачи, содержащихся в этой подзадаче.

Для каждой вновь полученной подзадачи оценка снизу будет не меньше, чем оценка родительской подзадачи, так как в нее входит только часть решений.

4)   Получение верхней оценки. Любое решение исходной задачи называют верхней оценкой. Верхняя оценка больше (хуже) или равна оптимальному решению.

5)   Отсечения. Если для подзадачи нижняя оценка получилась больше или равна верхней оценке, то эта подзадача заведомо не содержит решения лучше одного из уже найденных решений. Поэтому дальнейшее ее исследование не имеет смысла. Идущий от нее фрагмент дерева отсекается. Чем больше ветвей дерева отсекается, тем быстрее работает МВГ. А отсечения зависят как от качества нижних оценок, так и от качества верхней оценки (исходного размещения).

6)   Ветвление. Чаще всего используется следующий способ ветвления:

-        для подзадач верхнего уровня получают оценки снизу;

-        подзадача с лучшей оценкой разбивается на подзадачи следующего уровня, и для них определяются оценки снизу;

-        эти подзадачи добавляются к тем подзадачам, от которых еще не производилось ветвление, из них выбирается для разбиения подзадача с лучшей нижней оценкой;

-        если таких подзадач несколько, то из них выбирается самого низкого уровня, если и их несколько, то выбор производится случайно.

Сформулируем МВГ для задачи размещения элементов.

Дерево решений будем строить закрепляя элемент за элементом в определенных ячейках. Подзадачи первого уровня получим, закрепляя первый элемент в каждой из ячеек, 2-го уровня – второй элемент в оставшихся свободных ячейках и т.д.

Верхнюю оценку получим, используя начальное размещение.

Трансформация задачи будет заключаться в том, что разрешается перераспределять часть связей между элементами, но так, что бы суммарная длина связей не увеличивалась (тогда решения исходной задачи входят в решения трансформированной задачи, а оптимальное решение подзадач является их нижней оценкой).

Рассмотрим один из способов получения нижней оценки. Суммарная длина связей:

. Если наименьший элемент матрицы R умножить на наибольший элемент матрицы D, наименьший из оставшихся элементов матрицы R на наибольший из оставшихся элементов матрицы D, и т.д., а затем сложить полученные N² произведений, то полученный результат будет меньше или равен суммарной длине связей любой допустимой расстановки. Таким образом, это может служить нижней оценкой.

Когда часть элементов уже размещена, то суммарную длину связей можно разбить на три части:

, где

- длина связей уже размещенных элементов, это точное значение;

- длина связей между размещенными и не размещенными элементами, точное значение неизвестно, но можно найти оценку снизу;

   - длина связей между не размещенными элементами, точное значение неизвестно, но можно найти оценку снизу.

Тогда нижняя оценка для подзадачи: .

Рассмотрим пример работы МВГ.

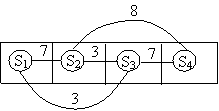В целях упрощения расчетов примем, что четыре элемента расположены в линейке ячеек:

 

 

 

 

Расстояние между соседними ячейками равно 1. Начальная расстановка указана на рисунке. Матрица смежности:

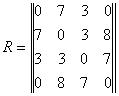,          матрица длин:

Начальная расстановка дает оценку сверху .

Первый этап – закрепление первого элемента последовательно по всем ячейкам.

Задача 1.  , т.к. размещен только один элемент.

Считаем : из первой строки матрицы  вычеркиваем первый член (0) и упорядочиваем оставшиеся по возрастанию (0,3,7). То же самое делаем для матрицы , но упорядочиваем по убыванию. (3,2,1)

Замечание:  чтобы найти  необходимо для каждого размещенного элемента найти оценку снизу длины его связей с не размещенными элементами. - номер элемента, - номер ячейки, в которой он размещен. Из строки  матрицы  вычеркиваем все размещенные элементы (вектор упорядочиваем по возрастанию). Из строки  матрицы  вычеркиваем все занятые ячейки (вектор упорядочиваем по убыванию). Выполняем скалярное произведение векторов.

Считаем . Из матриц  и  вычеркиваем первую строку и первый столбец. Из над диагональных членов формируем два вектора (3,7,8) и (2,1,1):

, тогда .

Задача 2. , то есть первый элемент закрепляем за второй ячейкой. .

. Для подсчета  из матрицы  вычеркиваем первый столбец и первую строку, из матрицы  вычеркиваем второй столбец и вторую строку:

. Тогда .

Задача 3. , то есть первый элемент закрепляем за третьей ячейкой.

.  .  .

.

Задача 4. . .  .  .

.

Второй этап. Будем закреплять второй элемент в каждой из свободных ячеек. Первый элемент закрепим за ячейкой 1 (оценки снизу для задач N1 и N2). Ветви от задач N2 и N3 отсекаются, так как для них оценки снизу хуже оценки сверху.

Задача 5. ,   (помещаем второй элемент во вторую ячейку).

.

Считаем . Теперь для каждого размещенного элемента надо подсчитать связи с не размещенными элементами.

Из первой строки матрицы  вычеркиваем два первых члена, получим вектор (0,3). Из первой строки матрицы  вычеркиваем два первых члена, получим вектор (3,2):

.

Из второй строки  вычеркиваем два первых члена: (3,8). Из второй строки  вычеркиваем два первых члена: (2,1).

.

.

Считаем . Из  и  вычеркиваем два первых столбца и две первых строки, получим вектора: (7) и (1): .

Тогда: .

Задача 6. ,  .

. 

,  , .  .

 (отсекаем эту ветвь).

Задача 7. ,  .

.

,  , .  .

  (отсекаем).

Третий этап. Закрепление третьего элемента. Так как элементов – 4 и ячеек 4, то закрепление третьего элемента автоматически приводит к закреплению четвертого элемента, то есть на третьем этапе мы попадаем на концевые вершины. Решение трансформированной задачи на концевых вершинах совпадает с решением исходной задачи. У нас остались две необрезанные ветви от задач N4 и N5. Выбираем N5, так как она более низкого уровня.

Задача 8. ,  , ,  ().

 (уже считали).

Задача 9. ,  , ,  ().

.

.

У нас осталась еще одна необрезанная ветвь от задачи 4, лгко убедиться, что решив ее, получим симметричное решение: .