1. Моделирование переходных процессов.

Под расчетом (моделированием) переходных процессов в схеме подразумевают необходимость определения токов и напряжений в любой точке схемы в заданные моменты времени.

Если цепь содержит индуктивности L или емкости C , то аналитически параметры цепи, зависящие от времени можно рассчитать только путем решения дифференциальных уравнений. На рисунке 1 показан простой пример такой цепи, в которой емкость подключается к источнику постоянного напряжения.

В начальный момент времени t = 0, u_c = u_c0. При постоянной времени τ = RC, аналитическое решение выглядит следующим образом:

.                                     (1.1)

При использовании ЭВМ для решения дифференциальных уравнений используются численные методы. В этом случае мгновенные значения каждого параметра цепи определяются только для дискретных моментов времени. На основании начальных условий (t = 0) вычисляются параметры цепи сначала в момент t₁, затем в моменты t₂, t₃, … и так далее, до требуемого момента времени. Каждый параметр вычисляется на основании значений, полученных в предыдущие моменты времени. Например, напряжение u₁, определяется на основании известного u_c0 , а u_c2 на основании рассчитанного u_c1 (рисунок 2).

В общем случае обозначим последние уже вычисленные значения параметров цепи индексом n, а еще неизвестные параметры, которые предстоит определить на следующем шаге – индексом n + 1. Интервал времени h, равный:

h = t_n+1 - t_n                            (1.2)

называется шагом интегрирования. В общем случае шаг интегрирования может изменяться при расчете переходного процесса.

При расчете переходных процессов цепи с несколькими реактивными элементами необходимо для каждого момента времени решить систему обыкновенных дифференциальных уравнений.

Разработано достаточно много численных методов решения систем дифференциальных уравнений. Наиболее известные из них: явный метод Эйлера, метод трапеций, неявный метод Эйлера.

Рассмотрим в качестве примера дифференциальное уравнение первого порядка:

                                   (1.3)

Требуется найти функцию x(t), при известных начальных условиях, удовлетворяющую уравнению (1.3).

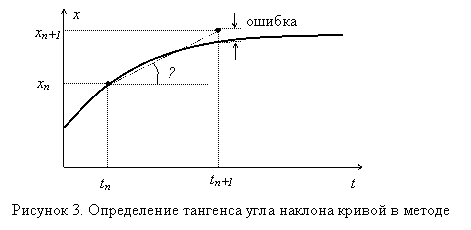
Функцию x(t) между точками t_n и t_n+1 можно аппроксимировать прямой линией с тангенсом угла наклона α, равным:

                               (1.4)

Уравнение (1.4 ) описывает производную как в момент времени t_n:

                            (1.5)

так и в момент времени t_n+1:

                         (1.6)

В явном методе Эйлера очередное значение функции x(t) вычисляется по выражению полученному из (1.5):

                         (1.7)

Значение , рассчитывается по исходному уравнению (1.3) на каждом шаге. Метод, называется явным, так как неизвестная есть только в одной части (уже имеется.).

В неявном методе Эйлера очередное значение функции x(t) вычисляется по выражению полученному из (1.6):

                     (1.8)

Так как в обеих частях уравнения есть неизвестные, метод называется неявным. В этом случае приходится на каждом шаге решать уравнение (1.8), относительно x_n+1.

Основное преимущество неявных методов: отсутствие ограничений на шаг интегрирования (или эти ограничения незначительны). Поэтому в программах СМ нашел применение неявный метод Эйлера (метод первого порядка), а также методы второго порядка (метод трапеций, он же – модифицированный метод Эйлера) и другие.

Опуская некоторые теоретические рассуждения, отметим, что для решения численным методом системы дифференциальных уравнений моделируемой схемы в базисе узловых потенциалов компонентные дифференциальные или интегральные уравнения необходимо привести к дискретному виду. Напомним, компонентные уравнения для емкости и индуктивности в базисе узловых потенциалов имеют вид:

    ;                                (1.9)

Для решения неявным методом Эйлера дискретизированные формулы можно представить в следующем виде:

;               ;                                (1.10)

где компоненты  и  играют роль фиктивных проводимостей для емкости и индуктивности соответственно.

При решении задачи в базисе узловых потенциалов, вектор токов составляется на основе уравнений (1.10), если ветвь содержит емкость или индуктивность. При этом значения  и заменяются через разности потенциалов, а значения  и  предполагаются известными из предыдущих вычислений или начальных условий.

Дискретные схемы замещения, соответствующие выражениям (10) показаны на рисунке 4.

При формировании матрицы узловых проводимостей G вклад каждой емкости или индуктивности равен их фиктивной проводимости с соответствующими знаками.

Таким образом, для решения задачи численными методами, заменяем реактивные элементы их дискретными моделями и приходим к системе конечно-разностных (не дифференциальных)  уравнений, в общем случае нелинейной (если схема содержит еще и нелинейные элементы). Процесс перехода от дифференциальных уравнений к их конечно-разностным аппроксимациям называется алгебраизацией.

В этом случае теоретическая модель схемы в базисе узловых потенциалов имеет вид:

.                  (1.11)

где  - вектор поправок,   - матрица проводимостей (матрица Якоби); k – номер ньютоновской итерации, n – номер текущего (уже рассчитанного) момента времени.

Итак, вычислительный процесс расчета переходных процессов в схеме состоит из следующих процедур:

1. Составляем модель схемы в форме уравнений (1.11), заменяя реактивные элементы схемы их дискретными моделями (вид которых зависит от метода интегрирования).

2. На первом шаге интегрирования, исходя из начальных условий и заданного шага интегрирования h, решаем систему (1.11), в общем случае нелинейных уравнений, методом Ньютона. Напомним, что на каждой итерации по методу Ньютона решается система линейных уравнений (на каждой итерации ищутся поправки Δφ_n+1). В результате получаем значения узловых потенциалов для первого момента времени, отстоящего на h от начального.

3. Далее на очередном шаге полагаем, что , и снова решаем (1.11), относительно неизвестных φ_n+1 узловых потенциалов. Этот процесс повторяется до тех пор, пока не будет пройден заданный интервал времени.